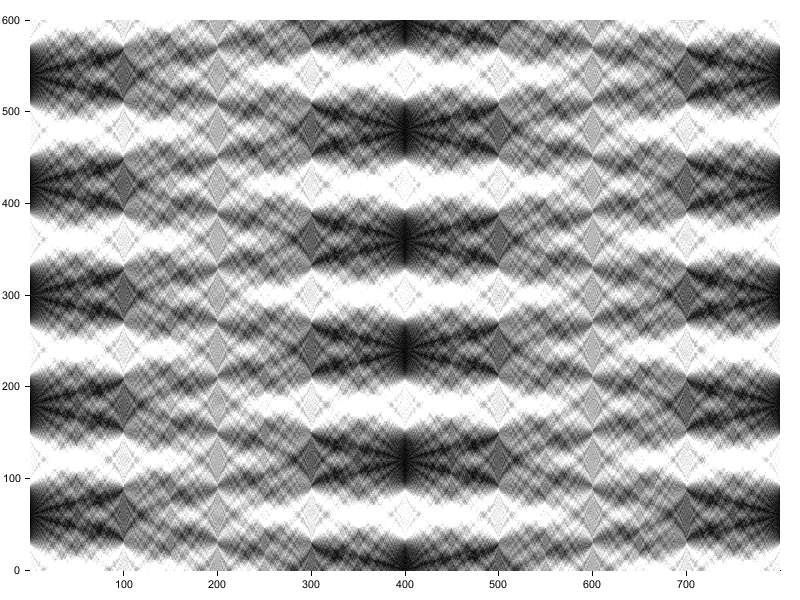
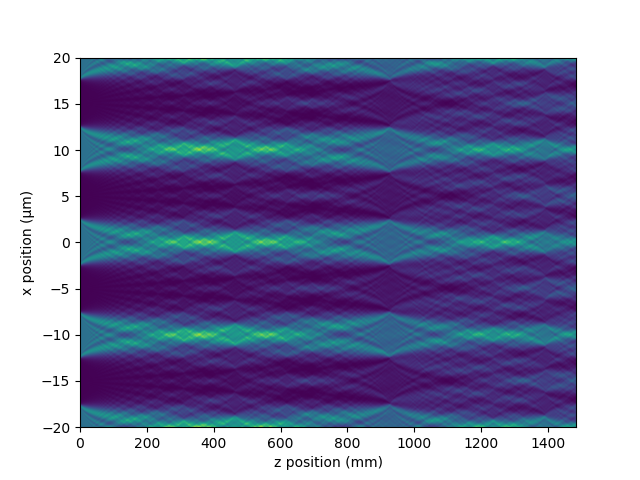
rosetta-carpet
The Talbot carpet in different languages.
julia
using Unitful
using Unitful.DefaultSymbols
using Unitful: keV, h, c
using FFTW
FFTW.set_num_threads(Sys.CPU_THREADS)
using PyPlot
# a struct to hold the simulation info
struct PropagationInfo
x
y
fx
fy
end
# utilities
"The rectangle function."
rect(x) = one(x) .* (abs.(x) .< 0.5)
"frequencies for which the fft is calculated"
fftfreq(n) = ifftshift(-cld(n-1, 2) : fld(n-1, 2)) / n
# physics
"Transfer function for the Fresnel free propagation."
H(fx, fy, λ, z) = exp(im * 2π / λ * z) .* exp(-im * π * λ * z * (fx^2 + fy^2))
#H(fx, fy, λ, z) = exp(im * 2π / λ * z) .* exp(im * 2π/λ / z * (fx^2 + fy^2)) / (im * λ * z)
# gratings
singrating(x, y, m, L) = 0.5(1 + m * cos.(2π * x / L))
rectgrating(x, y, m, L; th = 0) = 0.5(1 + m * sign.(cos.(2π * x / L) - th))
rectgrating(pp::PropagationInfo, m, L; th = 0) = rectgrating.(
pp.x, pp.y, m, L, th = th)
square(x, y, m, L) = m * rect(x / 2L) * rect(y / 2L)
circle(x, y, m, L) = m * rect(sqrt(x^2 + y^2) / 2L)
circle(pp::PropagationInfo, m, L) = circle.(pp.x, pp.y, m, L)
"Turns an amplitude grating into a phase one."
turn2phase(g) = exp.(im * π / 2 * g)
function fresnelgrid(;δx = 0.1e-6, δy = δx,
Nx = 2000, Ny = Nx, efficient = true)
if efficient
# FFTs are faster on arrays of lengths equal to powers of 2
Nx = nextprod([2], Nx)
Ny = nextprod([2], Ny)
end
# x are columns, y are rows
x = δx * (collect(1:Nx) .- Nx/2)'
y = δy * (collect(1:Ny) .- Ny/2)
fx = (fftfreq(length(x)) ./ δx)'
fy = fftfreq(length(y)) ./ δy
return PropagationInfo(x, y, fx, fy)
end
tonormalspace(U) = ifft(U, (1,2))
tofourierspace(u) = fft(u, (1,2))
flatwave(pp) = ones(ComplexF64, length(pp.y), length(pp.x))
"Propagate a wavefront in the Fourier space"
propagate(U, fx, fy, λ, z) = U .* H.(fx, fy, λ, z)
propagate(U, pp::PropagationInfo, λ, z) = propagate(U, pp.fx, pp.fy, λ, z)
propagatenormal(u, pp::PropagationInfo, λ, z) = tonormalspace(
propagate(tofourierspace(u), pp, λ, z))
pp = fresnelgrid(δx = 0.1μm, Nx = 4000, Ny = 1)
period = 10μm
g0 = rectgrating(pp, 1, period)
u1 = flatwave(pp) .* g0
λ = h * c / 46keV
u2(z) = propagatenormal(u1, pp, λ, z)
talbot_distance = 2period^2 / λ
z = reshape(collect(range(0mm, stop = 0.2talbot_distance, length = 2000)), 1, 1, :)
talbot_carpet = abs.(u2(z)).^2
plothunit = mm
plotvunit = μm
imshow(talbot_carpet[1, :, :],
interpolation = "bicubic",
origin="lower",
extent=[
ustrip(plothunit, z[1]), # left
ustrip(plothunit, z[end]), # right
ustrip(plotvunit, pp.x[1]), # bottom
ustrip(plotvunit, pp.x[end]) # top
],
aspect="auto")
xlabel("z position ($plothunit)")
ylabel("x position ($plotvunit)")
ylim(-20, 20)
savefig("$(dirname(dirname(@__FILE__)))/docs/carpets/julia.png")
rust
use plotters::prelude::*;
use std::convert::TryFrom;
use std::f64::consts::PI;
use rustfft::num_complex::Complex;
use rustfft::num_traits::Zero;
use rustfft::FFTplanner;
fn main() -> Result<(), Box<dyn std::error::Error>> {
let period: f64 = 10e-6;
let lambda = 26.95e-12;
let ny: usize = 600;
let nz: usize = 800;
let talbot_distance = 2. * period.powi(2) / lambda;
let dz = talbot_distance / nz as f64;
let dy = period * 5. / ny as f64;
let fy = fftfreq(ny, dy);
// The initial wavefront - rectangular grating
let g0: Vec<Complex<f64>> = (0..ny)
.map(|y| (y as f64) * dy)
.map(|y| 0.5 * (1. + (2. * PI * y / period).cos().signum()))
.map(|y| Complex::new(y, 0.))
.collect();
// prepare the FFT package, also for the inverse transform
let mut planner = FFTplanner::new(false);
let fft = planner.plan_fft(ny);
let mut iplanner = FFTplanner::<f64>::new(true);
let ifft = iplanner.plan_fft(ny);
let mut input: Vec<Complex<f64>> = vec![Complex::zero(); ny];
// where the carpet is stored
let mut z: Vec<Vec<Complex<f64>>> = vec![vec![Complex::zero(); ny]; nz];
z[0].copy_from_slice(&g0);
for iz in 1..nz {
// fft
input.copy_from_slice(&z[0]);
fft.process(&mut input, &mut z[iz]);
// processing in the Fourier space
for (v, f) in z[iz].iter_mut().zip(fy[..ny].iter()) {
// normalization
*v *= Complex::new(1.0 / (ny as f64), 0.0);
// transfer function for the Fresnel free propagation
let ddz = dz * iz as f64;
*v *= Complex::new(0., 2.0 * PI / lambda * ddz).exp();
*v *= Complex::new(0., -1. * PI * lambda * ddz * f.powi(2)).exp();
}
// inverse fft
input.copy_from_slice(&z[iz]);
ifft.process(&mut input, &mut z[iz]);
}
// plotting
let image_path = std::env::current_exe()?
.parent().expect("Wrong path.")
.parent().expect("Wrong path.")
.parent().expect("Wrong path.")
.parent().expect("Wrong path.")
.parent().expect("Wrong path.")
.join("docs")
.join("carpets")
.join("rust.png");
println!("{:?}", image_path);
let nz = u32::try_from(nz)?;
let ny = u32::try_from(ny)?;
let root =
BitMapBackend::new(&image_path, (nz, ny)).into_drawing_area();
root.fill(&White)?;
let mut chart = ChartBuilder::on(&root)
.margin(20)
.x_label_area_size(10)
.y_label_area_size(10)
.build_ranged(0..nz, 0..ny)?;
chart
.configure_mesh()
.disable_x_mesh()
.disable_y_mesh()
.draw()?;
let plotting_area = chart.plotting_area();
for xplot in 0..nz {
for yplot in 0..ny {
plotting_area.draw_pixel(
(xplot, yplot),
&HSLColor(0.0, 0.0, z[xplot as usize][yplot as usize].norm()))?;
}
}
Ok(())
}
fn fftfreq(n: usize, d: f64) -> Vec<f64> {
// ref. https://docs.scipy.org/doc/numpy/reference/generated/numpy.fft.fftfreq.html
let parity = n % 2;
let n = n as i32;
match parity {
// f = [0, 1, ..., n/2-1, -n/2, ..., -1] / (d*n) if n is even
0 => (0..n/2).chain(-n/2..0),
// f = [0, 1, ..., (n-1)/2, -(n-1)/2, ..., -1] / (d*n) if n is odd
1 => (0..(n-1)/2+1).chain(-(n-1)/2..0),
_ => panic!("i32 % 2 was neither 0 nor 1!")
}
.map(|f| f as f64 / (d * n as f64))
.collect()
}